History of Pythagoras Theorem

More than 4000 years ago, the Babyloneans and the Chinese already knew that a triangle with the sides of 3, 4 and 5 must be a right triangle. They used this knowledge to construct right angles. By dividing a string into twelve equal pieces and then laying it into a triangle so that one side is three, the second side four and the last side five sections long, they could easily construct a right angle

A Greek scholar named Pythagoras, who lived around 500 BC, was also fascinated by triangles with these special side ratios. He studied them a bit closer and found that the two shorter sides of the triangles squared and then added together, equal exactly the square of the longest side. And he proved that this doesn't only work for the special triangles, but for any right triangle. Today we would write it somehow like this: a² + b²= c². In the time of Pythagoras they didn't use letters yet to replace variables. (They weren't introduced until the 16th century by Vieta.) Instead they wrote down everything in words, like this: if you have a right triangle, the squares of the two sides adjacent to the right angle will always be equal to the square of the longest side.

Proofs of the Pythagorean Theorem

To give the Pythagorean Theorem in geometric terms we start with a right triangle abc. From the sides of this triangle we will draw squares from each of the sides, using the lengths of the sides as the length of a side for each respective square. The Pythagorean Theorem then claims that the sum of the areas of the two small squares equals (the area of) the large one.

In algebraic terms, a2+b2=c2 where c is the hypotenuse while a and b are the sides of the triangle.

The Pythagorean Theorem is probably the most well-known mathematical proofs, which many people remember well after their last course in mathematics.



Water-proof of Pythagoras' Theorem

Finding a Hypotenuse and a Short Side

Example1 Find the length of the hypotenuse of the right-angled triangle shown in the diagram.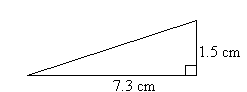
Solution: Let the length of the hypotenuse be x cm. By Pythagoras' Theorem,
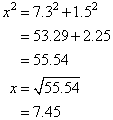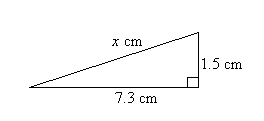So, the length of the hypotenuse is 7.45 cm. Example 2 Calculate the side-length missing from this diagram of a right-angled triangle. Solution: Let the missing side-length be x m, as shown. By Pythagoras' Theorem, So, the missing side-length is 2 Test Yourself: Pythagoras Exercise one http://www.subtangent.com/maths/ty-pythagoras.php Exercise Two http://www.cimt.plymouth.ac.uk/projects/mepres/book8/bk8i3/bk8_3i1.htm Exercise Three http://www.cimt.plymouth.ac.uk/projects/mepres/book8/bk8i3/bk8_3i2.htm

Pythagoras of Samos

            

Pythagoras of Samos was a famous Greek mathematician and philosopher, born between 580 and 572 BC, and died between 500 and 490 BC. He is known best for the Pythagorean theorem, which is an important theorem about right triangles. He started a group of mathematicians, called the Pythagoreans, who worshiped numbers and lived like monks. He was an influence for Plato.

He had a great impact on mathematics, theory of music and astronomy. His theories are still used in mathematics today. He was one of the greatest thinkers of his time.